NeurIPS'20 | BRP-NAS: Prediction-based NAS using GCNs

Abstract

The authors proposed BRP-NAS, an efficient hardware-aware NAS enabled by an accurate performance (latency and accuracy) predictor based on graph convolutional network (GCN). The BRP-NAS uses the binary relations of models and an iterative data selection strategy to improve the sample selection. In addition, they also released LatBench - a latency dataset of NAS-Bench-201 models running on abroad range of devices.

Background & Motivation

The performance of a neural network is captured by several metrics, such as accuracy, latency, and energy consumption. Because measuring performance metrics is expensive both in terms of time and computation, interest in predicting them has surged since neural architecture search was introduced.

For the latency prediction, most works rely on a proxy metric (e.g. FLOPS or model size) which is fast but inaccurate. More recently, layer-wise predictors have been proposed which effectively sum up the latencies of individual neural network layers. While being more accurate than the proxy, layer-wise predictors have a significant drawback: they do not capture the complexities of multiple layers executing on real hardware.

Most previous approaches which want to find the most accurate model that satisfies a strict latency constraint (e.g., for real-time applications) are limited entirely by the quality of latency estimation. Therefore, having a good latency predictor is significant.

Also, finding a good accuracy predictor is also important.

The goal of this paper is to find a solution to make the sample efficiency higher.

Contributions

• Latency prediction
• Accuracy prediction
• Towards reproducible research: latency benchmark

Approaches

Latency Prediction

The latency predictor uses 4 layers GCN, with 600 hidden units in each layer, followed by a fully connected layer that generates a scalar prediction of the latency. The input of GCN is the adjacency matrix (asymmetric as the computation flow is represented as a directed graph) and a feature matrix (one-hot encoding).

Accuracy Prediction

Transfer learning from latency predictors to improve accuracy predictors

The idea is that these GCN-based predictors for latency, accuracy and FLOPS have the same input representation. A trained GCN (e.g., for latency prediction) captures features of a model that are also useful for a similar GCN trained to predict a different metric (e.g., accuracy).

Therefore, we just need to initialize the weights of an accuracy predictor with those from a latency/FLOPS predictor. Then train the predictor using the validation accuracy of CIFAR-100 dataset.

Observations

The authors proposed a new predictor-based NAS according to the following observations:

1. Accuracy prediction is not necessarily required to produce faithful estimates (in the absolute sense) as long as the predicted accuracy preserves the ranking of the models;
2. Any antisymmetric, transitive and connex binary relation produces a linear ordering of its domain, implying that NAS could be solved by learning binary relations, where $O(n^2)$ training samples can be used from $n measurements;
3. Accurately predicting the rankings of top candidates is the most important.

Training predictor via iterative data selection

Given a budget of $T$ models and $I$ iterations, we start by randomly sampling and training $T/I$ models from the search space, and the results are used to train the initial version of the predictor. At the beginning of each subsequent iteration, we use the predictor to estimate the accuracy of all the models, denoted by M, in the search space. We then select the top $α ∗T/I$ unique models and randomly pick another $(1 −α) ∗T/I$ models from the top $M/2^i$models where $α$ is a factor between 0 and 1 and i is the iteration counter. The selected $T/I$ models are trained and their resulting accuracies are used to further train the predictor for the next iteration.

Binary relation predictor-based NAS (BRP-NAS)

The predictor reuses the GCN part of the latency predictor, without any changes, to generate graph embeddings for both input models. The embeddings are then concatenated and passed to a fully connected layer which produces a 2-valued vector. The vector is then passed through a softmax function to construct a simple probability distribution $p = (p1,p2) ∈R^2$ with $p1$ being the probability of the first model better than the second, and $p2$ being the probability of the opposite. The produced probability distribution is then compared to the target probability distribution obtained by taking a softmax of the ground-truth accuracy of the two models $(T1,T2)$, and the objective is to minimize the KL divergence between the two distributions. The overall network structure and the loss function are summarized in Figure 4.

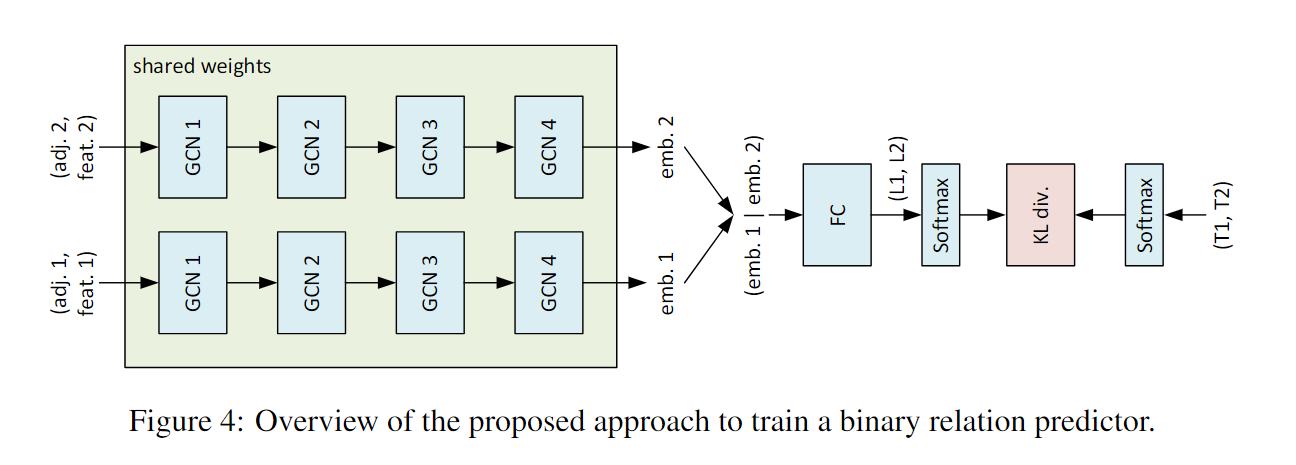
BRP-NAS consists of two phases. In the first phase, the ranking of all candidate models is predicted based on the outputs from a binary relation predictor, which is trained to predict the binary relation(accuracy comparisons between two models). In the second phase, based on the predicted rankings, models with high predicted ranks are fully trained, after which, the model with the highest trained accuracy is selected.

Results

The proposed predictors significantly improve the sample efficiency of NAS. Details can be checked in the paper.

Discussion

• Symmetry and transitivity of the learned binary relation.
• Generalization to other metrics and problems.