PPoPP'21 | A Fast Work-Efficient SSSP Algorithm for GPUs

Abstract

This paper presents a new Single Source Shortest Path (SSSP) algorithm for GPUs. The key advancement is an improved work scheduler, which is central to the performance of SSSP algorithms. Previous solutions yield poor work efficiency and can underutilize the hardware due to a lack of parallelism. The solution from this paper (Asynchronous Dynamic Delta-Stepping, ADDS) introduces a more sophisticated work scheduler-based on a novel highly parallel approximate priority queue that produces high quality schedules while being efficiently implementable on GPUs. In experiment, ADDS has 2.9x speed up compared to previous state-of-the-art solution.

Background & Introduction

Dijkstra’s algorithm and Bellman-Ford(BF)’s algorithm are the two most famous algorithms in SSSP search. For the Dijkstra, it can be optimized by the priority queue (Fibonacci heap). So it can achieve $O(vlogv+e)$ time complexity at most. For the BF, it do the relax operation for all edges, and repeats until the distances are coverage. BF has $O(ev)$ complexity. Dijkstra has lower time complexity and higher work efficiency (fewer edges touched), while BF has a better potential for parallelism. The delta-stepping gets a balance between work efficiency and parallelism. The idea of delta-stepping is shown in the following figure.

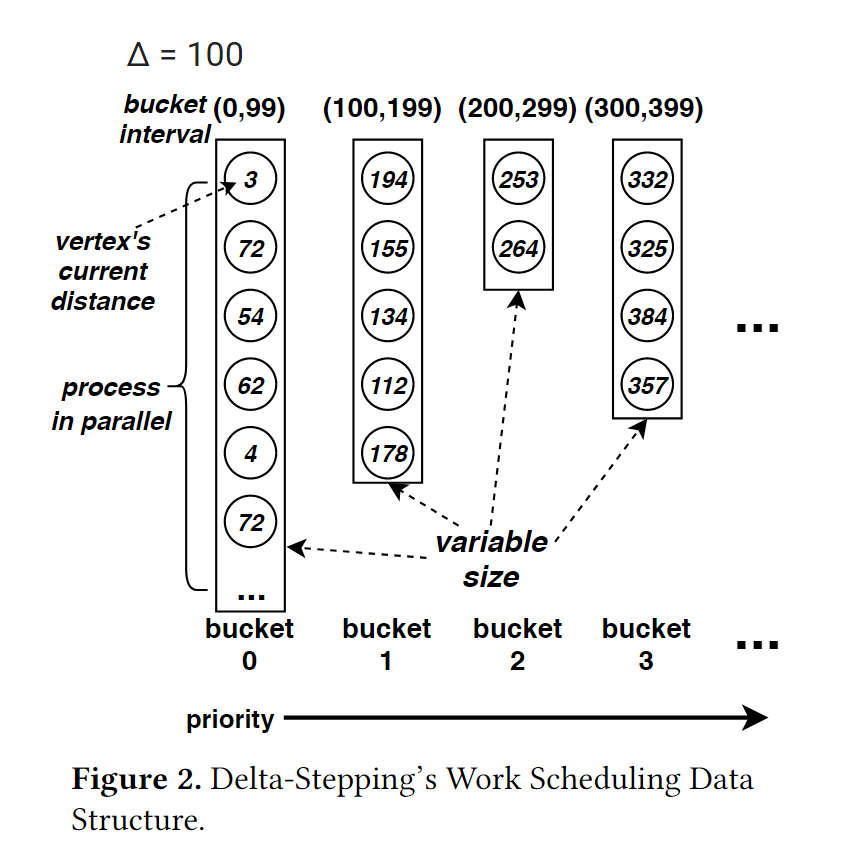
Delta-stepping uses multiple buckets to get priority. The vertices in the highest bucket can be processed in parallel. As an example in Fig. 2, the delta value is set to 100. So the vertices with a distance less than 100 will be put in bucket 0 (highest priority bucket). The vertices in bucket 0 will be processed in parallel first. The vertices with distances from 100 to 199 will be put in bucket 1, and so on.

However, If we want to implement delta-stepping on GPUs, we need to invoke a lot of sync and sort, which hurts the throughput of the GPU. The previous best solution is Near Far Pile[1], an adaptation of delta-stepping that makes several GPU-friendly simplifications to the worklist. First, it uses just two buckets, known as Near and Far, which can be implemented using pre-allocated arrays, thereby avoiding the need to perform dynamic memory management. Second, it uses the Bulk Synchronous Parallel (BSP) model in which an algorithm proceeds in a series of super steps separated by barrier synchronization. This model allows each bucket to be double buffered, with writes made to one buffer and reads made to a second buffer, greatly simplifying synchronization.

Unfortunately, Near-Far has three deficiencies.

1. Because it uses just two buckets, Near-Far provides an extremely coarse-grained approximation of a priority queue, leading to poor work efficiency.
2. Its use of barrier synchronization and double buffering severely limits parallelism, particularly for high-diameter graphs.
3. The granularity of the priority queue—that is, the range of priorities represented by each bucket, known as the Delta value—is chosen using a simple offline method that does not adequately capture important characteristics of the input graph and its relation to available parallelism.

In this paper, authors present ADDS (Asynchronous Dynamic Delta-Stepping), a novel formulation of delta-stepping that introduces an efficient worklist for GPUs to address the three deficiencies of Near-Far:

• It uses multiple buckets, which improves work efficiency.
• Instead of using the BSP model, it operates asynchronously, which avoids barrier synchronization and increases parallelism.
• It uses a dynamically selected Delta value that is chosen based on runtime information.

Design

Considerations

Three design considerations are:

1. Memory Management. We seek a worklist data structure that can efficiently grow and shrink the sizes of individual buckets as the program executes, without limiting the number of buckets to some small constant.
2. Synchronization. If multiple threads can read from and write to the same buckets, then we have MWMR access, which in general is not scalable on GPUs. Thus, many GPU SSSP algorithms, such as Near-Far, employ double-buffering, so that in any iteration of the algorithm, threads read from one buffer and write to another, removing the need for reader-writer synchronization. However, double buffering reduces concurrency, since newly generated work items can only be read in the next iteration, even if idle threads are available to perform the read. Double buffering is particularly harmful to high-diameter graphs, where the execution is forced into many tiny iterations. Thus, the challenge is to provide parallel access to buckets without resorting to synchronous double-buffering.
3. Granularity. A smaller Δ value produces finer-grained buckets that improve work efficiency but reduce parallelism. The optimal choice depends on the characteristics of both the input graph and the underlying hardware, since it depends on the weights and connectivity of the graph and the hardware’s available parallelism. Thus, Selecting the best value of Δ at runtime is a considerable solution.

Solution

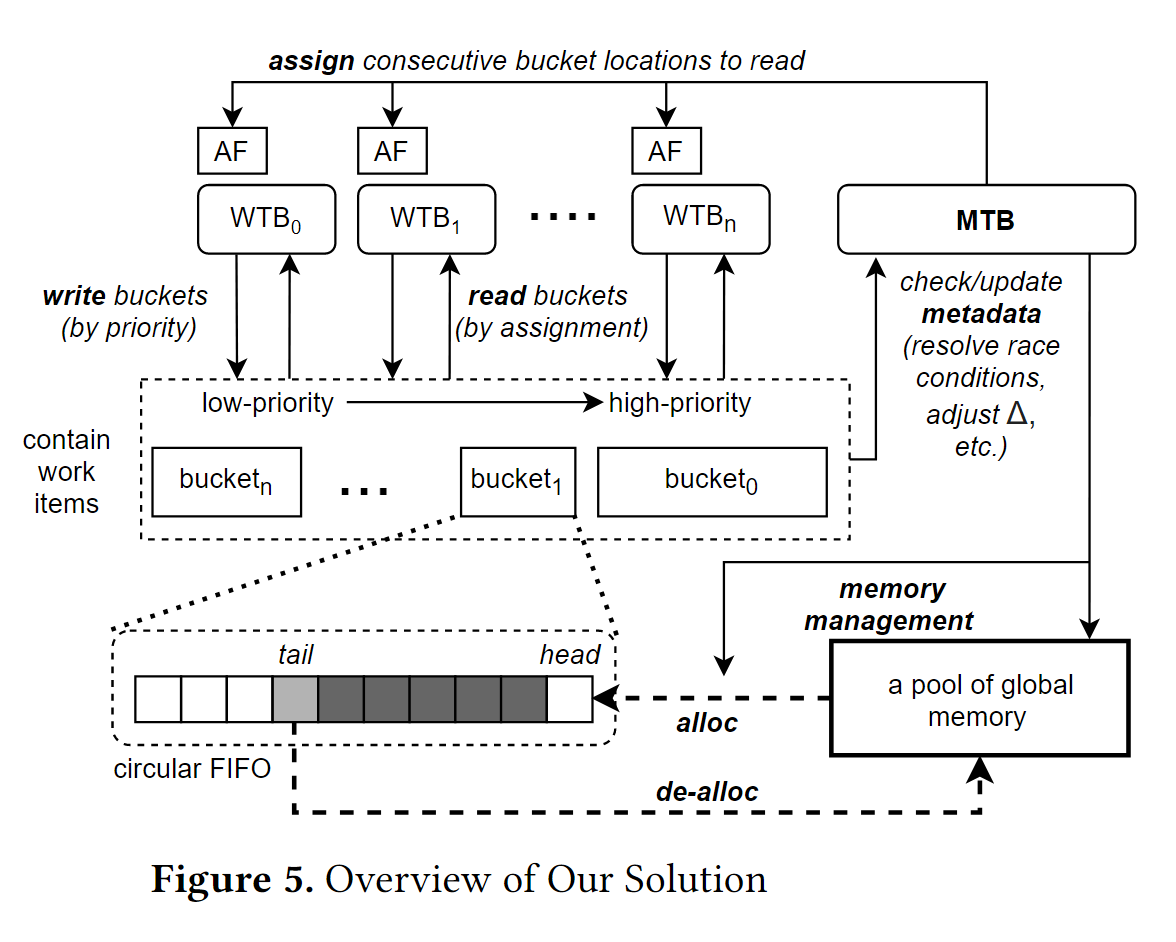
The overview of ADDS is shown in the following figure. The solution is a GPU adaptation of delta-stepping that introduces a new work scheduling mechanism that substantially improves work efficiency and parallelism. There are three keys to our solution.

1. ADDS uses a highly parallel approximate priority queue with dynamically sized buckets and customized memory management, which allows using many buckets instead of just two; this finer-grained priority queue improves work efficiency.
2. Instead of using double buffering, our bucket data structure efficiently supports asynchronous concurrent access by large numbers of worker threads, which significantly improves parallelism.
3. ADDS scheduler gathers runtime information to dynamically identify more suitable values of Δ.

Basic operation

The key to the solution is a delegation strategy in which worker thread blocks (WTBs) process vertices and assign work items to buckets according to their priority, but they do not read items directly from buckets. Instead, a single manager thread block (MTB) reads the buckets and assigns work items to worker threads. Thus, while the overall work queue has MRMW functionality, the metadata managed by the MTB ensures that the many WTBs do not write to the same memory locations. And the synchronization typically associated with MRMW access to the work queue is replaced by a simpler SRMW synchronization to the work queue metadata.

Once available work items are known, the MTB assigns this work to WTBs using a dedicated assignment flag (AF) for each WTB (see Figure 5). In addition to indicating whether the WTB is currently idle, an AF also contains the location and size of the array of work items that are assigned to the WTB when it is not idle. Each idle WTB polls its respective AF in scratchpad memory and thus receives work from the MTB without contention with other WTBs.

SRMW Queue Access Management

WTB threads can add work directly to a bucket; hence there are multiple writers. Work is added to these buckets in a lightweight manner by maintaining in the bucket’s metadata a reservation pointer (resv_ptr) that is accessed atomically by the WTBs. The resv_ptr is atomically incremented, and each accessing WTB is returned a unique index into the bucket array where it can place new work items without contention. Likewise, the MTB maintains a read pointer (read_ptr) to indicate the location in the queue at which it should start reading work items.

To avoid a race condition, we must ensure that as the MTB performs queue management and work distribution, it does not attempt to access work from locations that have not yet had work items written to them. Each MTB thread operates on an N-word segment of a bucket. Each segment is associated with a write completed counter(WCC), which is initially 0. When a WTB thread writes a work item into the location at its unique bucket index, it executes a memory fence to ensure that the item is fully written and then atomically increments the WCC for the segment into which it is writing. The WCC value is introduced to guarantee that the value of resv_ptr is not stale, the result is compared to resv_ptr after performing a memory fence operation.

Memory Management

To allow a bucket to grow and shrink dynamically, memory for a bucket is allocated in blocks of 64K 32 bit words. An array of pointers to allocated blocks is maintained for each bucket. The high order 16 bits of each 32 bit index are treated as an index into the pointer array, and the lower order 16 bits are an offset into the particular block (Similar to OS page index).

Managing the Ordered Work Queue

ADDS’s work queue consists of a fixed number of 32 buckets, managed as a circular priority queue with bucket priorities that increase from the tail (initially index 0) to the head (initially index 31). When the highest priority bucket becomes empty, the MTB increments the head and tail pointers so that the empty bucket can be reused.

In addition, performance can be optimized by allowing the MTB to allocate work from multiple high-priority buckets, instead of just the head bucket.

Dynamically Setting the Δ Value

The value of Δ can significantly impact performance. For some graphs, the best performance delta is close to the best work efficiency delta, while for the other graphs, they are very far. ADDS leverages a runtime method that automatically selects a point near best-perf-point for a given graph. Before execution starts, it chooses an initial Δ value using a heuristic. Then it takes into account the effect of memory access divergence on bandwidth usage by correlating the number of threads with the average degree of the input graph. During execution, the MTB adjusts Δ to keep the utilization ensuring that the hardware is near full utilization.

Evaluation

For the 226 input graphs, ADDS achieves average speedup of 2.9× over the previous state-of-the-art work. The acceleration comes from the improvement of both work efficiency and parallelism. (RTX 2080Ti)

[1] Andrew Davidson, Sean Baxter, Michael Garland, & John D. Owens (2014). Work-Efficient Parallel GPU Methods for Single-Source Shortest Paths international parallel and distributed processing symposium.